Download Soal KSN SMA 2020 Bidang Matematika Tingkat Provinsi
Pada kesempatan ini m4th-lab akan membagikan soal Kompetisi Sains Nasional Tingkat Provinsi (KSN-P) Bidang matematika jenjang SMA. Untuk soal KSN 2020 Tingkat SMA sudah kami bagikan di sini.
Kompetisi Sains Nasional SMA tingkat Provinsi tahun 2020 dilaksanakan secara online. Soal kompetisi terdiri dari 5 soal uraian yang terbagi ke dalam dua bagian. Pada bagian pertama peserta diberikan 3 soal uraian dan pada bagian kedua peserta diberikan 2 soal uraian. Berikut ini soal Kompetisi Sains Nasional SMA tahun 2020 Bidang Matematika:
Uraian Bagian Pertama
Soal 1
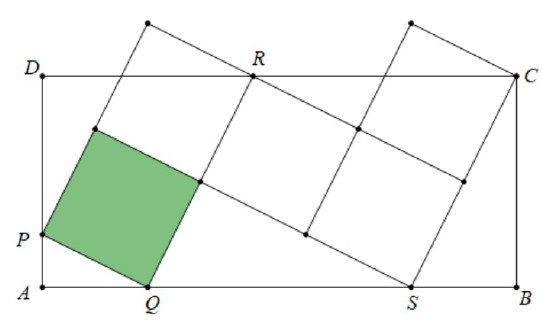
Diberikan lima persegi kecil dan sebuah persegi panjang besar $ABCD$ seperti pada gambar berikut ini.
Dalam gambar tersebut, titik $P, Q, R, S$ terletak pada sisi persegi panjang $ABCD$. Jika diketahui bahwa luas persegi kecil adalah 1 satuan, tentukan luas persegi panjang $ABCD$
Soal 2
Diberikan fungsi kuadrat $f(x)=x^2+px+q$ dengan $p$ dan $q$ merupakan bilangan bulat. Misalkan $s$, $b$, dan $c$ adalah bilangan bulat berbeda sehingga $2^{2020}$ habis membagi $f(a)$, $f(b)$ dan $f(c)$, tetapi $2^{1000}$ tidak habis membagi $b-a$ dan juga tidak habis membagi $c-a$. Tunjukkan bahwa $2^{1021}$ habis membagi $b-c$
Soal 3
Tentukan semua bilangan irasional $x$ sehingga $x^2+20x+20$ dan $x^3-2020x+1$ keduanya merupakan bilangan rasional
Uraian Bagian Kedua
Soal 4
Diketahui segitiga $ABC$ tidak sama kaki dengan garis tinggi $AA_{1}$, $BB_{1}$ dan $CC_{1}$. Misalkan $B_A$ dan $C_A$ berturut-turut titik pada $BB_1$ dan $CC_1$ sehingga $A_{1}B_{A}$ tegak lurus $BB_1$ dan $A_1C_A$ tegak lurus $CC_1$. Garis $B_AC_A$ dan $BC$ berpotongan di titik $T_A$. Definisikan dengan cara yang sama titik $T_B$ dan $T_C$. Buktikan bahwa $T_A$, $T_B$ dan $T_C$ kolinear.
Soal 5
Di suatu kota, $n$ anak mengikuti kompetisi matematika dengan nilai total berupa bilangan bulat non negatif. Misalkan $k<n$ bilangan bulat positif. Untuk setiap anak $s$, ia mendapatkan:
- $k$ buah permen untuk setiap poin nilai yang diperolehnya, dan
- untuk setiap anak lain $t$ yang nilainya lebih tinggi dari $s$, maka $s$ mendapatkan 1 buah permen untuk setiap poin selisih nilai $t$ dan $s$.
Setelah semua permen dibagikan, ternyata tidak ada anak yang memperoleh permen lebih sedikit dari Badu, dan ada $i$ anak yang memperoleh nilai lebih tinggi dari Badu. Tentukan semua nilai $i$ yang mungkin.
Demikianlah soal Kompetisi Sains Nasional Matematika SMA Tingkat Provinsi (KSN-P) Tahun 2020. Untuk mendownload soal tersebut dalam format pdf, link download kami sertakan di bawah preview berikut ini:
Semoga bermanfaat


Post a Comment